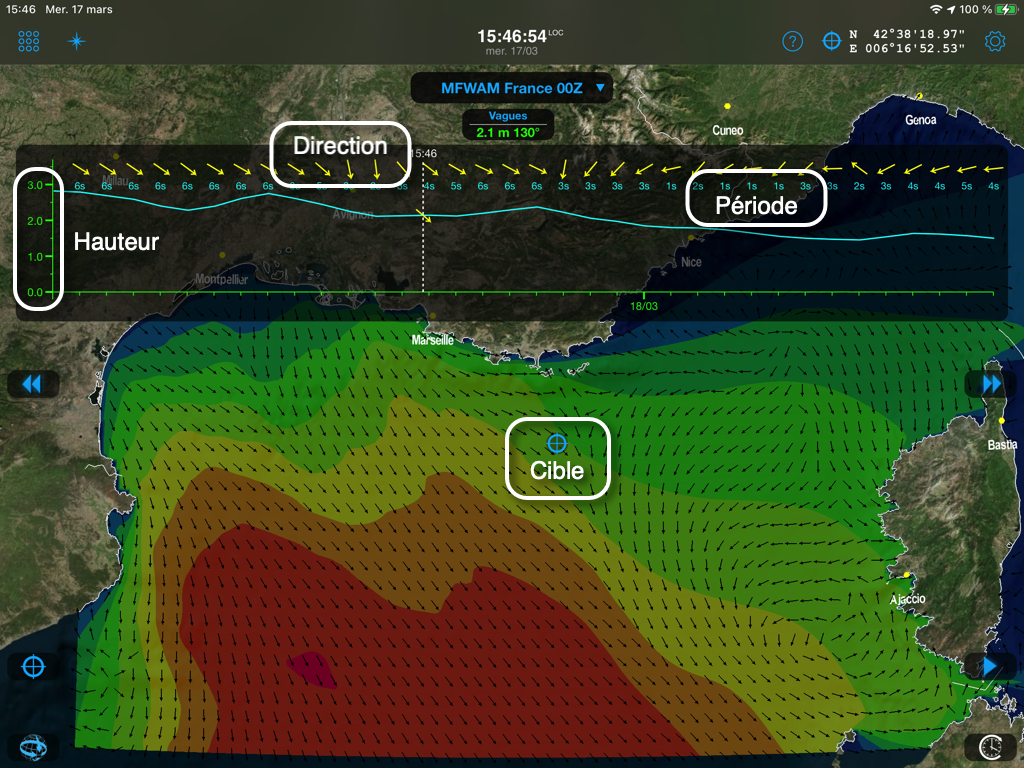
In Weather4D, as generally in other applications, sea state forecasts are described by ocean models. The most used is the model WW3 (Wave Watch III), published by FNMOC (Fleet Numerical Meteorology and Oceanography Center) of the US Navy, with a global model due to 7 days and resolution 1° (60NM), and a Europe model to 3 days and resolution 0.2° (12NM). Météo-France publish the models MFAUM (Wave Assimilated Model) coupled with the ARPEGE and AROME weather models with three resolutions : Global at 0.5° (30NM), Europe at 0.1° (6NM), France at 0.025° (1,5NM) with variable deadlines (¹).
Each of these models provides three essential data for navigation (among several dozen other oceanographic data) : the height, the direction and period waves. This is the “sea of wind” from associated weather models.
However, these three data raise some questions : what relationship between height and period, can we predict if the waves break, what reliability when approaching the coast ? Let's try to answer it (²) …
Wave propagation medium
We must first distinguish two wave propagation environments. : in deep water (dispersive environment) and shallow water (non-dispersive environment). Only the deep sea environment will be discussed here, far from the coasts and the rise of the seabed.
We determine the notion of dispersive environment by a ratio between the wavelength of the waves (The) and the depth of the sea (P). Without going into mathematical details, to simplify the propagation in deep water we consider, i.e. where the waves are not affected by the bottom, when P > L/2 or L<2P, which amounts to the same. For example, with a wavelength of 150m, the depth must be greater than 75m. With a sounding at 60m, the wavelength must not exceed 120m.
Wave characteristics
 The Period (T) is the time interval between two crests, or two hollows, expressed in seconds. In deep water, the Wavelength (The) expressed in meters is equal to 1,5T². Example : waves of 8 period seconds will have a wavelength of 1.5×8² = 96m (≅ 100m). The Velocity, or speed of propagation, is equal to 1,5T expressed in meters per second. In the example, 1,5×8 = 12 m/s (23 knots). The Height is the vertical distance from the crest to the hollow, expressed in meters.
The Period (T) is the time interval between two crests, or two hollows, expressed in seconds. In deep water, the Wavelength (The) expressed in meters is equal to 1,5T². Example : waves of 8 period seconds will have a wavelength of 1.5×8² = 96m (≅ 100m). The Velocity, or speed of propagation, is equal to 1,5T expressed in meters per second. In the example, 1,5×8 = 12 m/s (23 knots). The Height is the vertical distance from the crest to the hollow, expressed in meters.
The values of these data are closely related to the wind force, to the expanse over which the wind blows, called generating area, and the distance over which the wind is blowing without encountering an obstacle, called the fetch.
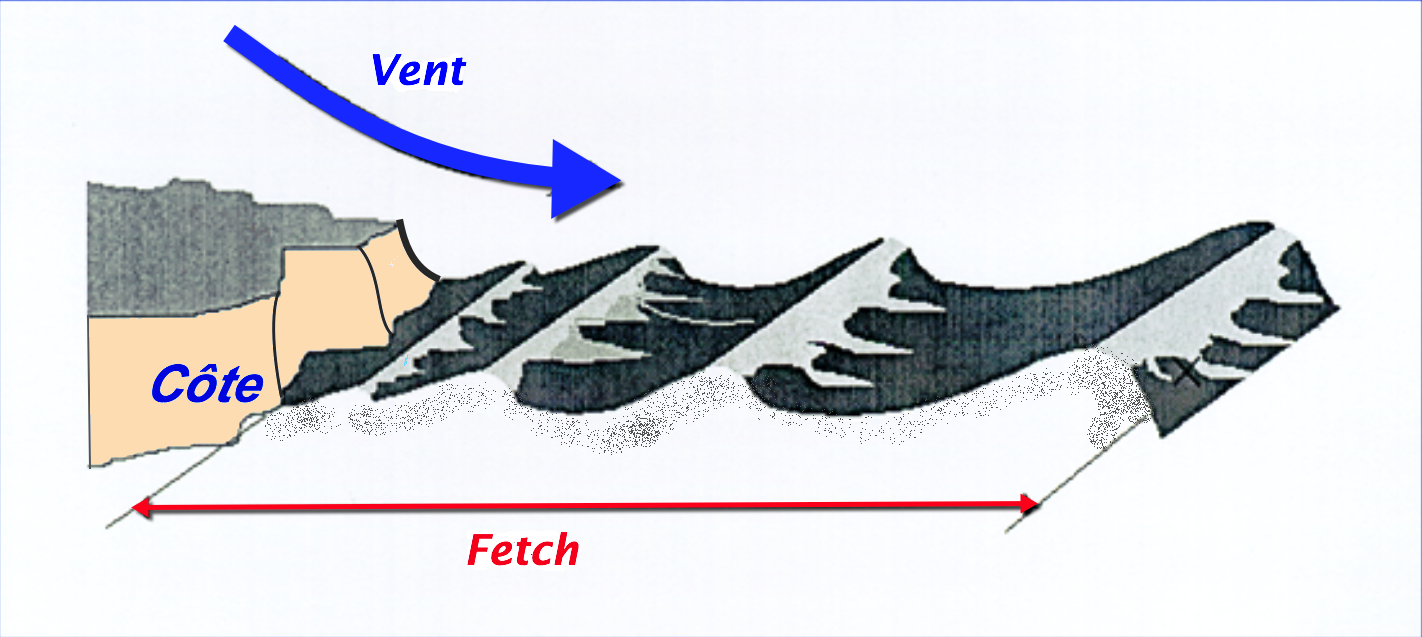
The unobstructed distance over which the wind is blowing
Wave trains
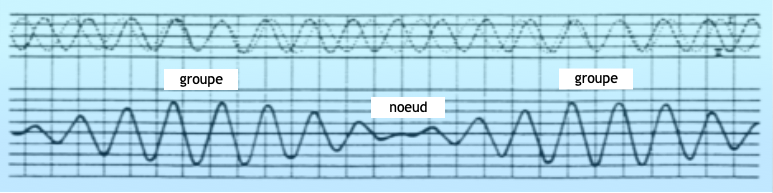
The state of the sea is often made up of the superposition of several wave systems.. Groups are formed by the combination of wave trains of the same height and direction, but having slightly different periods. The waves will thus move in groups whose speed in deep water will be approximately half the speed of each isolated wave.. The speed of the group is therefore calculated V = C/2, i.e. V = 1.5T/2 = 0,75T. Example : the speed of a group of waves whose period is 8 seconds will be 1.5×8/2 = 6m/s (12 knots). We therefore observe cyclically groups of steeper waves, the heights being added, and significantly lower wave intervals.
The surge
The breaking of a wave is determined by the notion of Camber (γ). This data is defined by the formula γ=H/L, or the ratio of wave height to wavelength. We demonstrate by calculation that the wave breaks, in deep water, when the camber γ>0,14. This limit value can be reached, either by the force of the wind alone, either by the wind against a strong current (in the Channel, in example, when the tide turns against the wind), by the crossing of wave trains of different directions, or by a rising sea floor (in the latter case we enter a non-dispersive environment).
Example with waves of H=5m and T=6s, limited breaking risk :
-
-
- L = 1,5T² = 1,5×6² = 54m
- γ = H/L = 5/54 = 0,09
-
We can easily calculate, for each wave height, the limit period giving a camber γ>0,14. Here are some examples :
| Height | Calculated period | Rounded period |
| 5meters | 4,88s. | 5s. |
| 6meters | 5,35s. | 5,5s. |
| 8meters | 6,2s. | 6,5s. |
| 10meters | 6,9s. | 7s. |
But be careful, we must not confuse “breaking wave” and “breaking crest” which occurs much earlier, from 30-35 knots of wind, when gusts sweep over the tops of waves as in the illustration below. On the other hand, in the wave groups mentioned previously, at the same period, groups of steeper waves can reach heights causing a limit camber.
As you approach the coast, things get complicated. Wave calculations in a non-dispersive environment, therefore at shallow depth, become more complex and are the subject of numerous specialist literature, to which I do not belong. Each of us knows perfectly well that the rise of the continental shelf causes a significant worsening of the state of the sea during strong westerly winds., even more on the Channel when the tide is against, and that the Tramontana can form a breaking swell on the northern coasts of the Balearic Islands, as in the following illustration.
Such a situation makes surfers happy !
–––
(¹) See, for more details, the User manuals of Weather4D to download for free.
(²) Source : General and Maritime Meteorology, Météo-France – 2001
–––




Thank you Francis